최근 수정:
Binary Search Tree. 한글로 이진 탐색 트리.
데이터들을 빠르게 탐색, 삽입, 삭제 하기 위해 만든 자료구조 중의 하나이며, 성능도 나름 좋고 구현도 꽤나 간단하여 많이 쓰인다.
이진 트리의 구조를 가지며, 부모를 기준으로 왼쪽 자식들은 부모보다 항상 작아야 하며 오른쪽 자식들은 부모보다 항상 커야 한다는 규칙을 가진다. 이런 특성은 이용하면 탐색, 삽입, 삭제가 로그 시간복잡도가 되어 매우 효율적이다. (일반 배열이나 리스트는 선형 시간복잡도이다)
하지만, 이진 탐색 트리의 단점은 데이터를 삽입 시, 거의 정렬된 데이터가 들어오게 되면 일반 배열과 다를 게 없으므로 효율이 매우 떨어진다. 이를 보완하기 위해 2-3-4 트리나 레드 블랙 트리 등을 사용한다.
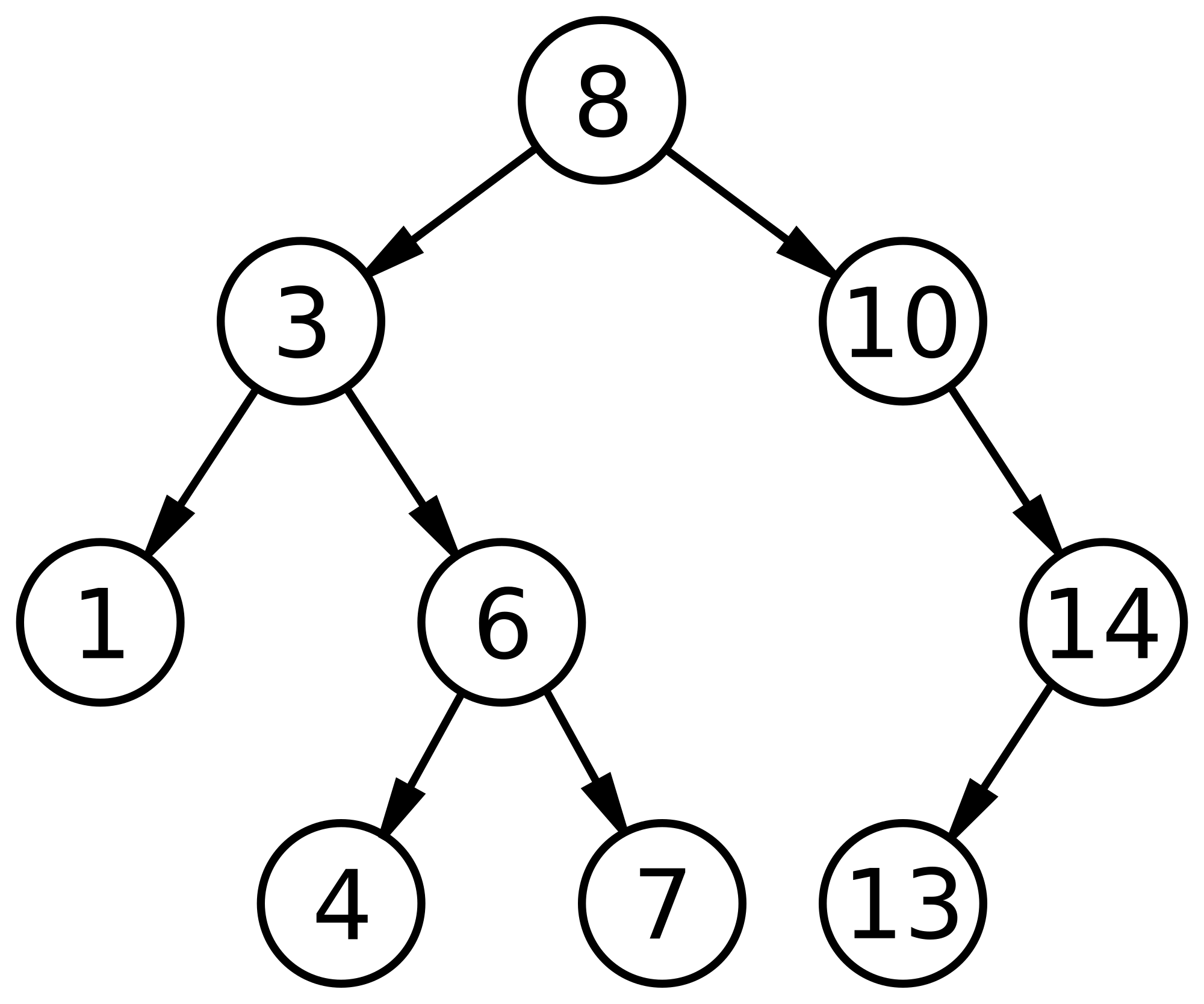
간단하게 탐색, 삽입, 삭제에 대해 설명하겠다. 아래 트리 그림 참고 바람.

찾고자 하는 값이 7이라면,
먼저 루트, 8과 비교해서 더 작으므로 왼쪽으로
3보단 크므로 오른쪽으로
6보다도 크니까 오른쪽으로 가면 탐색 완료!
탐색이랑 거의 비슷하다.
삽입하고자 하는 값이 9라면,
먼저 루트, 8과 비교해서 더 크므로 오른쪽으로
10보단 작으므로 왼쪽으로
근데 10노드의 왼쪽엔 자식이 없기 때문에 여기에 9 노드를 생성하여 붙여준다.
가장 까다롭다.
자식 개수에 따라 경우를 3가지로 나눠야 함. (자식이 0개, 1개 또는 2개.)
0개일 경우 그냥 삭제하면 됨.
1개일 경우도 삭제하고 자식을 부모에다 붙여주면 됨.
그러나 2개일 경우엔….(3 삭제)
왼쪽 자식들 중 가장 큰 값을 붙이거나
오른쪽 자식들 중 가장 작은 값을 붙여야 함.
3을 삭제한다면 왼쪽에서 가장 큰 1
또는 오른쪽에서 가장 작은 4 값을 3 자리에 붙여준다.